一：平衡二叉树：

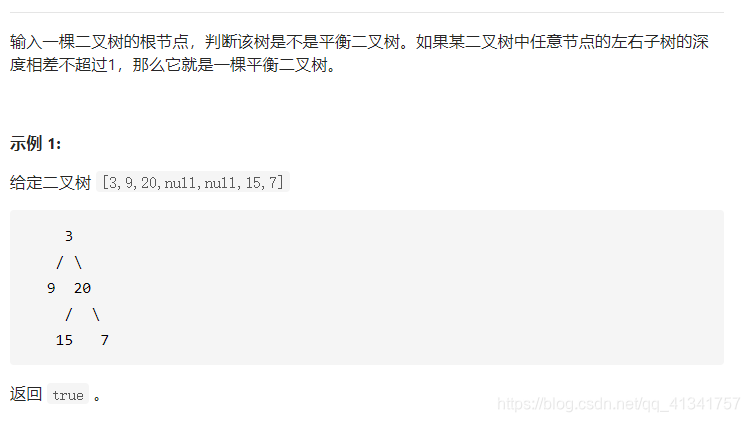
class Solution:
    # 求树的高度采用DFS算法：
    # 先递归左子树再递归右子树
    def dfs(self, root):
        if root == None:
            return True
        return max(self.dfs(root.left), self.dfs(root.right)) + 1


    def isBalanced(self, root: TreeNode) -> bool:
        # 1：如果是空树则肯定是平衡二叉树
        if root ==None:
            return True
        # 2：自顶向下，每次先求出左子树高度和右子树高度，然后判断高度差是不是1或0
        left_deep = self.dfs(root.left)
        right_deep = self.dfs(root.right)
        if (left_deep - right_deep) not in [-1, 0, 1]:
            return False
        # 3：如果高度差满足了，还要保证左子树跟右子树也要是平衡二叉树，因此递归调用。
        return self.isBalanced(root.left) and self.isBalanced(root.right)

二：二叉树的深度：

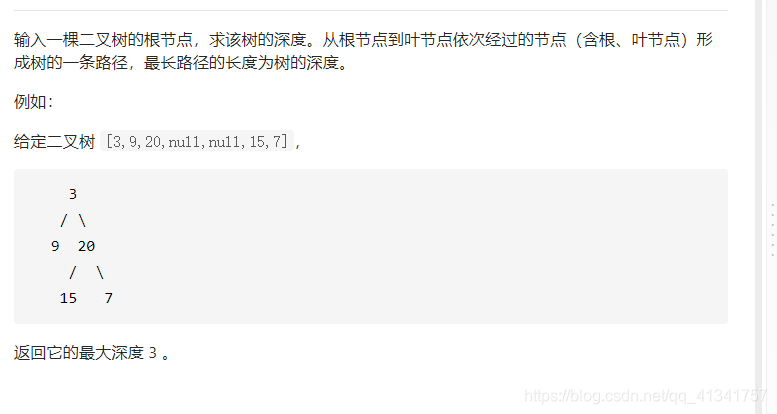
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if root == None:
            return 0
        return (max(self.maxDepth(root.left), self.maxDepth(root.right))) + 1

三：对称二叉树：

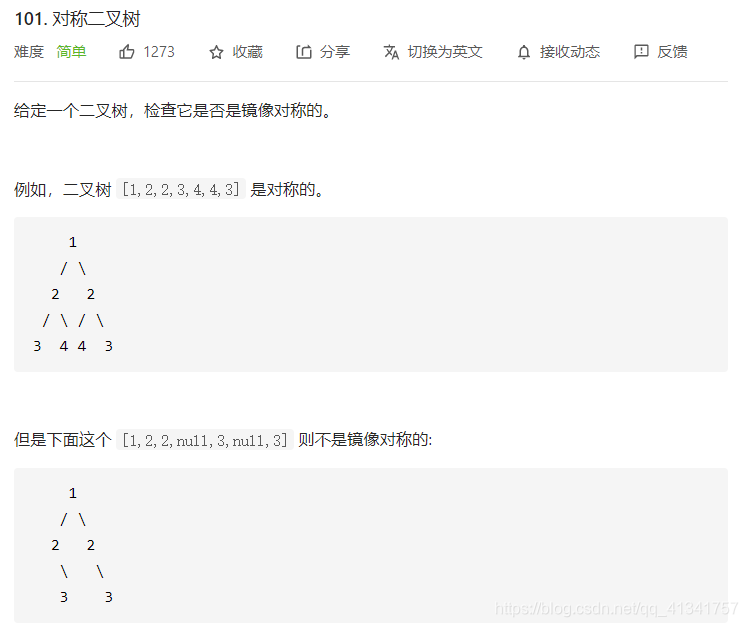
class Solution:
    # 使用DFS判断是否是镜像对称
    def dfs(self, left_root, right_root):
        # 1： 递归边界,两个都是None，则返回True
        if left_root == None and right_root == None:
            return True
        # 2: 如果其中一个是None,则返回False
        if left_root == None and right_root != None:
            return False
        if left_root != None and right_root == None:
            return False
        # 3: 如果两个树跟值相等，A的左子树=B的右子树， A的右子树 = B的左子树，则返回true
        if left_root != None and right_root != None:
            return left_root.val == right_root.val and self.dfs(left_root.left, right_root.right) and  self.dfs(left_root.right, right_root.left)

    def isSymmetric(self, root: TreeNode) -> bool:
        # 1: 如果空树则肯定镜像对称
        if root == None:
            return True
        # 2： 调用DFS判断是否是镜像对称
        return self.dfs(root.left, root.right)

四：判断两棵树是否相同：

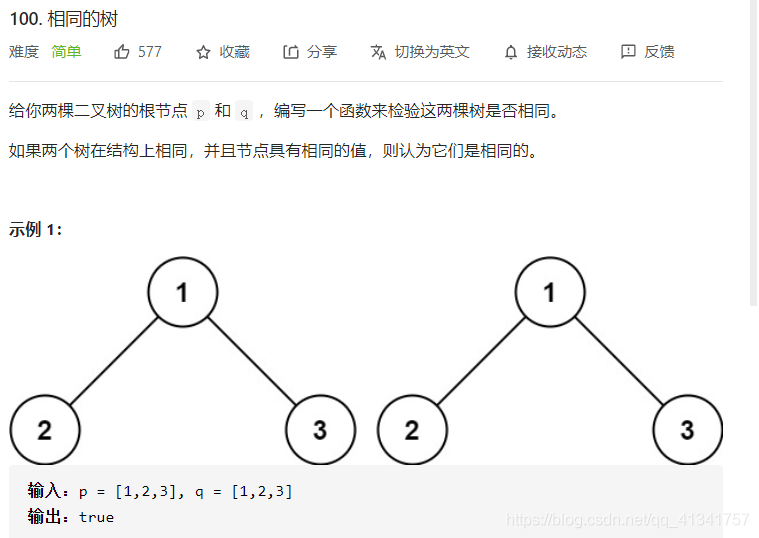
class Solution:
    # dfs判断两棵树是否相同
    def dfs(self, root1, root2):
        # 1: 递归终点
        if root1 == None and root2 == None:
            return True
        if root1 == None and root2 != None:
            return False
        if root1 != None and root2 == None:
            return False
        # 2: 一般性递归： 判断两个根节点是否相等，左子树等否相等，右子树是否相等
        return root1.val == root2.val and self.dfs(root1.left, root2.left) and self.dfs(root1.right, root2.right)

    def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
        # 1:如果一个是空树，另外一个不是则返回Flase
        if p == None and q!= None:
            return False
        if p != None and q == None:
            return False
        if p == None and q == None:
            return True
        # 2： 如果不是特殊情况调用DFS判断两个树是否相同
        return self.dfs(p, q)

五：二叉搜索树的范围和：

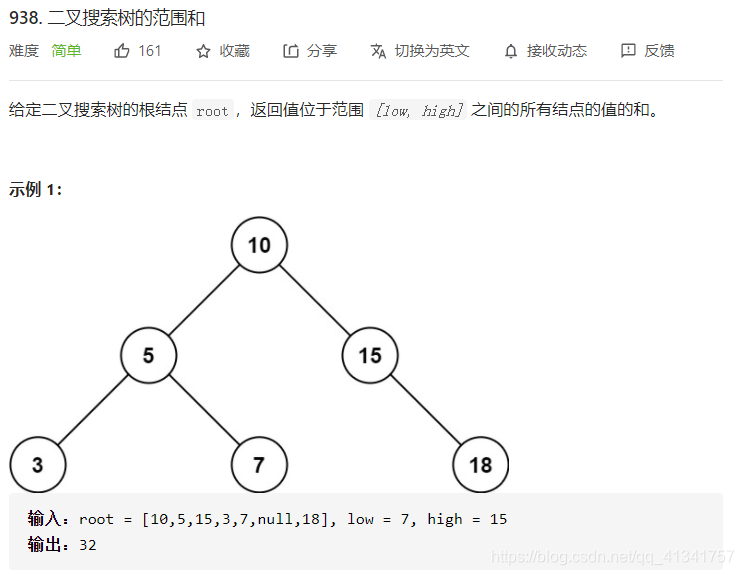
class Solution:
    # 实例变量保存加和
    def __init__(self):
        self.sum_num = 0
        self.low = 0
        self.high = 0

    # 深度优先遍历，返回范围内的累加和
    def dfs(self, root):
        # 1: 递归边界：
        if root == None:
            return 
        # 2: 正常情况：对结点的值判断
        if root.val >= self.low and root.val <= self.high:
            self.sum_num += root.val
        # 3: 左递归和右递归
        self.dfs(root.left)
        self.dfs(root.right)


    def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
        # 1: 特殊如果是空树，则直接返回None
        if root == None:
            return 0
        # 2: 一般情况进行深度优先遍历
        self.low = low
        self.high = high
        self.dfs(root)
        return self.sum_num

六：路径总和：

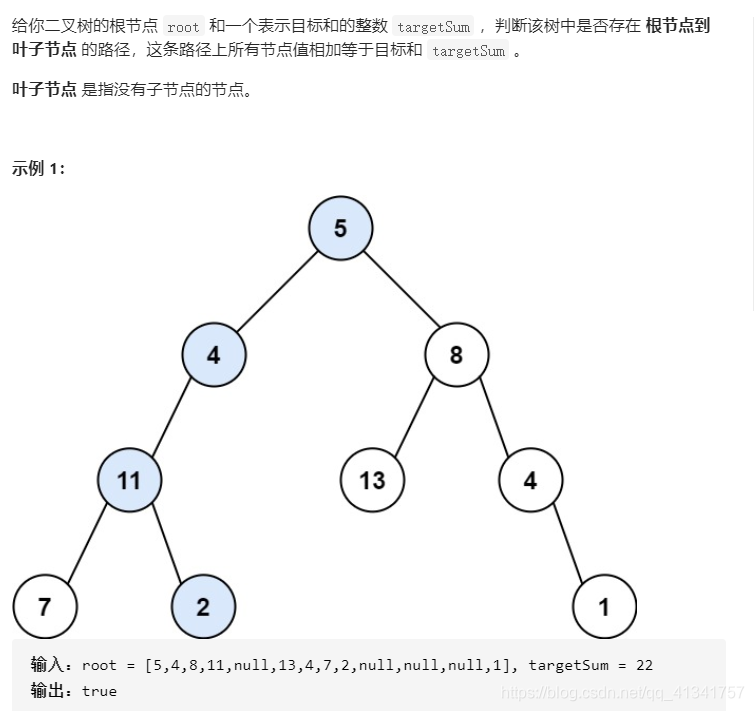
class Solution:
    def __init__(self):
        self.flag = False

    def dfs(self, root, targetSum):
        # 递归边界（叶子节点 + 路径整好是targetsum）
        if root.left == None and root.right == None and targetSum - root.val == 0:
            self.flag = True
        
        # 一般情况： 进行左右递归
        if root.left: 
            self.dfs(root.left, targetSum - root.val)
        if root.right:
            self.dfs(root.right, targetSum - root.val)
    
    def hasPathSum(self, root: TreeNode, targetSum: int) -> bool:
        # 1: 如果是个空树，则直接返回False
        if root == None: 
            return False
        
        # 2: 如果不是空树，则调用DFS判断是否存在这个路径
        self.dfs(root, targetSum)
        return self.flag

七：最小高度树：

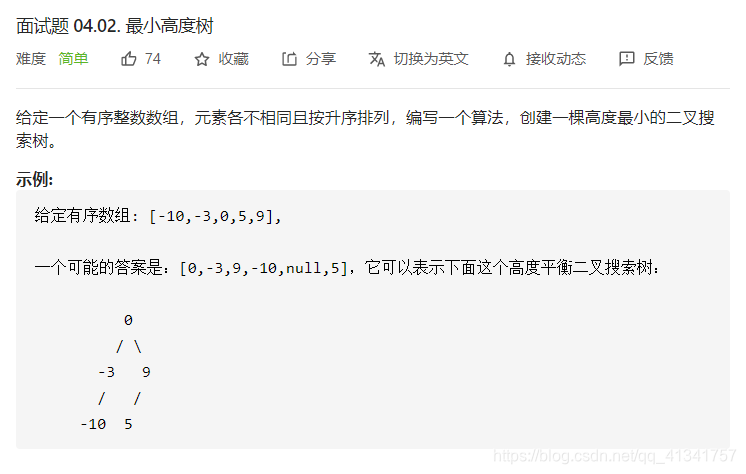
class Solution:

    # 使用DFS创建最小高度的二叉搜索树
    def dfs(self, nums):
        if not nums:
            return 
        mid = len(nums) // 2
        root = TreeNode(nums[mid])
        root.left = self.dfs(nums[: mid])
        root.right = self.dfs(nums[mid + 1: ])
        return root
        
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
         return self.dfs(nums)

八：二叉搜索树节点的最小距离：

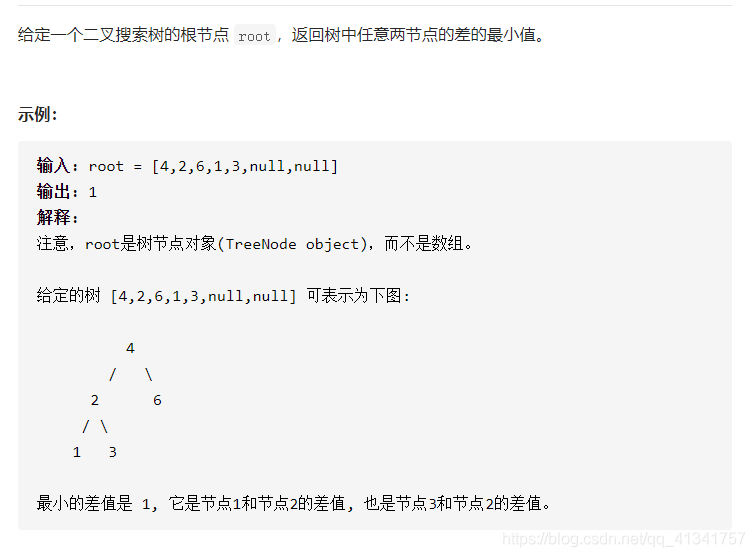
class Solution(object):
    def minDiffInBST(self, root):
        vals = []
        def dfs(node):
            if node:
                vals.append(node.val)
                dfs(node.left)
                dfs(node.right)

        dfs(root)
        vals.sort()
        return min(vals[i+1] - vals[i]
                   for i in range(len(vals) - 1))

九：N叉树的最大深度：

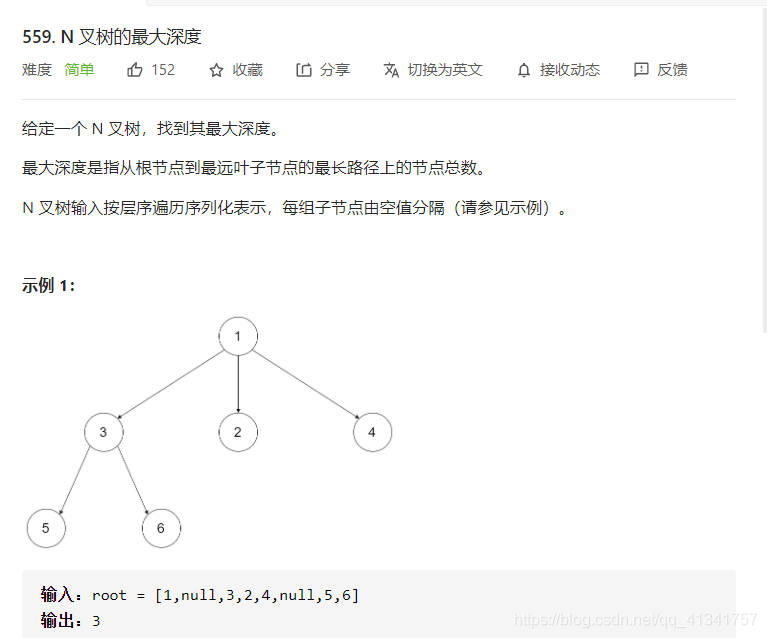
思路： 对于一个N叉树来说，我们可以用一个数组存储当前节点的子节点，然后遍历子节点的高度，选择最高的作为我们的当前根的高度。

class Solution:

    def dfs(self, root):
        if root is None: 
            return 0 
        elif root.children == []:
            return 1
        else: 
            height = [self.maxDepth(c) for c in root.children]
            return max(height) + 1 

    def maxDepth(self, root: 'Node') -> int:
        return self.dfs(root)