数学建模算法(基于matlab和python)之 变步长求积公式与龙贝格算法(3/10)
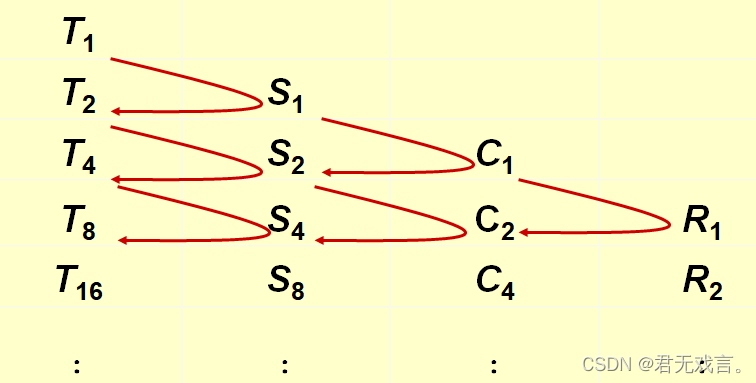
经过加工三次,就能得到精度较高得龙贝格值,且收敛速度加快很多,这种加速法称龙贝格算法。1、利用quad函数作变步长方法计算定积分。2、编写龙贝格方法计算定积分的程序并计算。的近似值,计算精度为。的近似值,计算精度为。利用变不长的梯形公式。
|
实验目的及要求:
|
||||||||||
|
实验内容: 1、利用quad函数作变步长方法计算定积分
2、编写龙贝格方法计算定积分的程序并计算 |
||||||||||
|
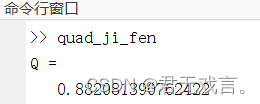
实验步骤与程序: 1.quad函数 quad函数的MATLAB主程序 F=inline('exp(-x.^2)'); Q=quad(F,0,2,10.^(-15)) 2.龙贝格方法计算定积分 算法分析 利用变不长的梯形公式
被调用的long_bei_ge.m文件 function [L,R,wu_cha,h]=long_bei_ge(fun,a,b,c) n=1;h=b-a; wu_cha=1;k=0; L=zeros(4,4); L(1,1)=h*(feval(fun,a)+feval(fun,b))/2; while(wu_cha>c) k=k+1; h=h/2; s=0; for j=1:n x=a+h*(2*j-1); s=s+feval(fun,x); end L(k+1,1)= L(k,1)/2+h*s; n=2*n; for i=1:k L(k+1,i+1)=((4^i)*L(k+1,i)-L(k,i))/(4^i-1); end wu_cha=abs(L(k+1,k)-L(k+1,k+1)); end R=L(k+1,k+1); %是其中L是龙贝格表,R是龙贝格值,wucha是误差估计,h是最小步长。 运行的long_bei_ge1.m文件 F=inline('exp(-x.^2)'); [L,R,wu_cha,h]=long_bei_ge(F,0,2,10.^(-15)) |
||||||||||
|
运行结果:
|
||||||||||
|
结果分析与讨论: |
||||||||||
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容

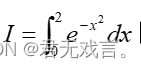 的近似值,计算精度为
的近似值,计算精度为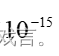 。
。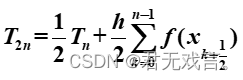 ,经过加工三次,就能得到精度较高得龙贝格值,且收敛速度加快很多,这种加速法称龙贝格算法。
,经过加工三次,就能得到精度较高得龙贝格值,且收敛速度加快很多,这种加速法称龙贝格算法。

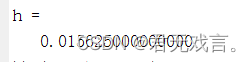








所有评论(0)